Qual o valor das seguintes equações do 2º grau. a) 3x² – 7x + 4 = 0 b) 9y² – 12y + 4 = 0 c) 5x² + 3x + 5 = 0
Respostas
Aline de Azevedo
há 6 anos
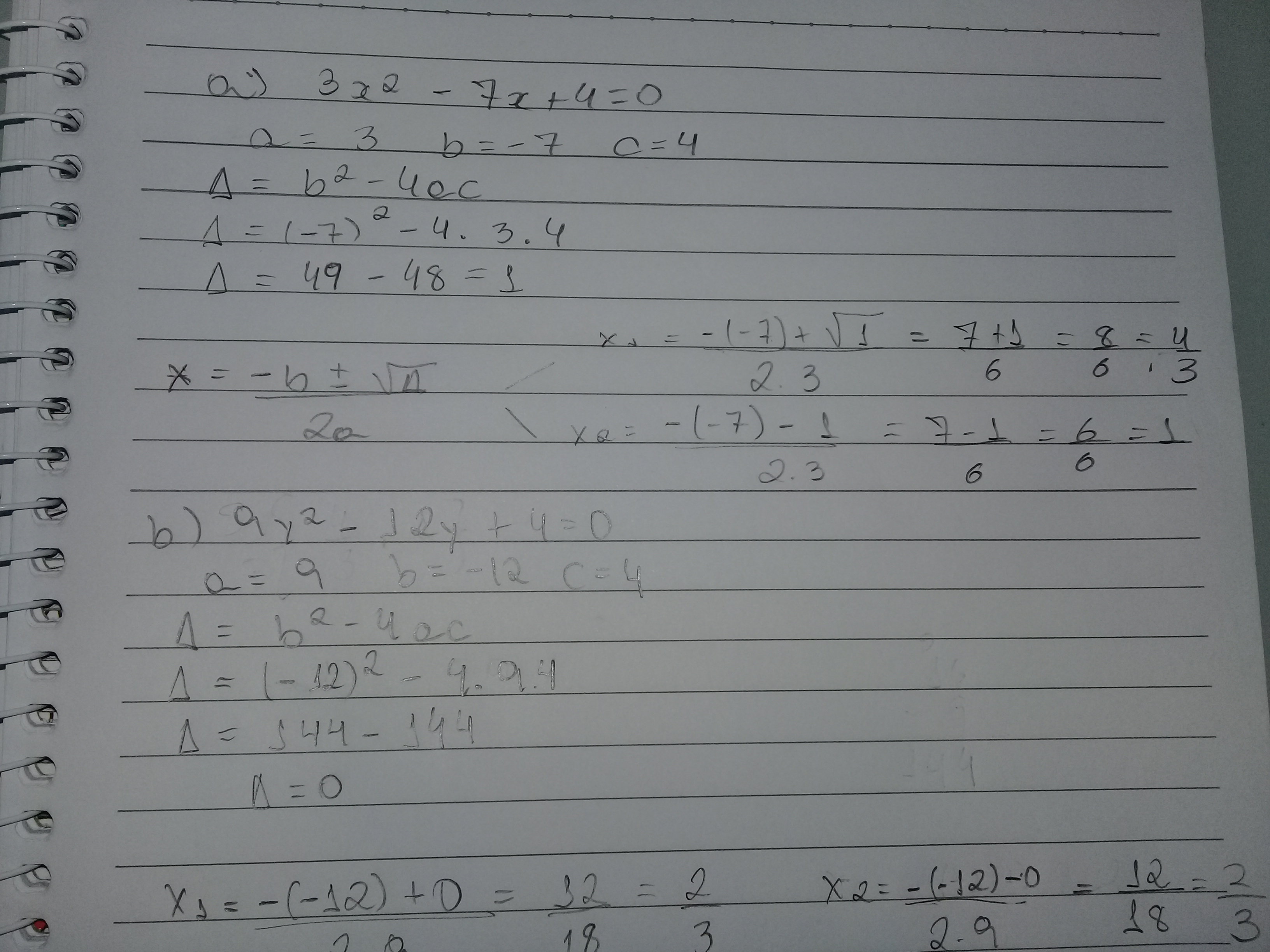



Crie sua conta grátis para liberar essa resposta. 🤩
Já tem uma conta?
Ao continuar, você aceita os Termos de Uso e Política de Privacidade
Andre Smaira
há 6 anos
\[\eqalign{ & x = \dfrac{{ - \left( { - 7} \right) \pm \sqrt {{{\left( { - 7} \right)}^2} - 4 \cdot 3 \cdot 4} }}{{2 \cdot 3}} \cr & = \dfrac{{7 \pm \sqrt 1 }}{6} \cr & = \dfrac{{7 \pm 1}}{6} \cr & \cr & \boxed{x' = \dfrac{8}{6}} \cr & \boxed{x'' = 2} }\]
b)
\[\eqalign{ & x = \dfrac{{ - \left( { - 12} \right) \pm \sqrt {{{\left( { - 12} \right)}^2} - 4 \cdot 9 \cdot 4} }}{{2 \cdot 9}} \cr & = \dfrac{{12 \pm \sqrt 0 }}{{18}} \cr & = \dfrac{{12 \pm 0}}{{18}} \cr & \cr & \boxed{x' = x'' = \dfrac{2}{3}} }\]
c)
\[\eqalign{ & x = \dfrac{{ - 3 \pm \sqrt {{{\left( 3 \right)}^2} - 4 \cdot 5 \cdot 5} }}{{2 \cdot 5}} \cr & = \dfrac{{ - 3 \pm \sqrt { - 91} }}{{10}} \cr & \cr & \boxed{x' = - \dfrac{1}{{10}}i\left( {\sqrt {91} - 3i} \right)} \cr & \boxed{x'' = \dfrac{1}{{10}}i\left( {\sqrt {91} + 3i} \right)} }\]





