Como podemos provar o teorema de pitagoras
💡 4 Respostas
Pablo Pereira
o teorema diz que a soma do quadrado dos lados e o valor da hipotenusa, so fazer a operacao inversa.
Andre Smaira
Nesse exercício vamos demonstrar o Teorema de Pitágoras.
Existem diversas formas de fazer essa demonstração. Vamos fazê-la por semelhança de triângulos usando a imagem abaixo:
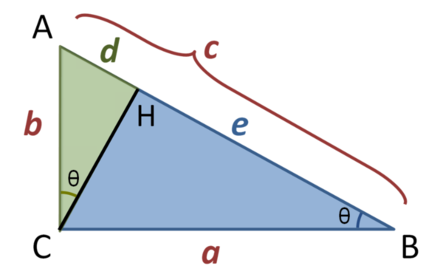
Da semelhança entre os triângulos ACB e CHB, temos:
$${a\over c}={e\over a}\Rightarrow a^2=ec$$
Da semelhança entre os triângulos ACB e AHC, temos:
$${b\over c}={d\over b}\Rightarrow b^2=dc$$
Somando os dois, temos:
$$a^2+b^2=(d+e)c=c^2$$
Como queríamos provar.
Andre Smaira
Nesse exercício vamos demonstrar o Teorema de Pitágoras.
Existem diversas formas de fazer essa demonstração. Vamos fazê-la por semelhança de triângulos usando a imagem abaixo:
Da semelhança entre os triângulos ACB e CHB, temos:
$${a\over c}={e\over a}\Rightarrow a^2=ec$$
Da semelhança entre os triângulos ACB e AHC, temos:
$${b\over c}={d\over b}\Rightarrow b^2=dc$$
Somando os dois, temos:
$$a^2+b^2=(d+e)c=c^2$$
Como queríamos provar.
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta








Compartilhar