De todas as soluções inteiras não negativas da equação x + y = 7, quantas são formadas por números primos

 os valores que x e y podem assumir são:

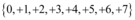
Desse conjunto de números, os únicos números que são primos são: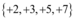 

Se x=2, então y=5 ( verdadeiro, e ambos números primos)

Se x=3, então y=4 ( verdadeiro, mas 4 não é um número primo)

Se x=5, então y=2 ( verdadeiro, e ambos números primos)

Se x=7, então y=0 ( verdadeiro, mas 0 não é um número primo)

Sendo assim, apenas duas soluções são formadas por números primos:

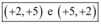
Conclusão:

Portanto, para a equação  , temos apenas duas soluções formadas por números primos, que são:

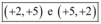
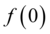
Contextualização:

Números primos são os números naturais que têm apenas dois divisores diferentes: o 1 e ele mesmo.

Exemplos:

1) 2 tem apenas os divisores 1 e 2, portanto 2 é um número primo.

2) 17 tem apenas os divisores 1 e 17, portanto 17 é um número primo.

3) 10 tem os divisores 1, 2, 5 e 10, portanto 10 não é um número primo.

Observações:

1 não é um número primo, porque ele tem apenas um divisor que é ele mesmo.

2 é o único número primo que é par.

Resolução:

Como x e y devem ser números inteiros não negativos, e a soma de