Determine os pontos críticos( primeira derivada =0) estude sua variação do sinal encontrando p ponto de inflexão e fazendo o estudo da concavidade. a)

x=4

Calcularemos primeiramente o ponto crítico para esta função:

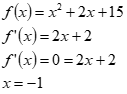
O ponto crítico ocorre então em x=-1. Para analisar a concavidade, basta calcularmos um valor logo antes e logo após o ponto crítico, e observarmos a variação da função neste local (pode ser em f(x) mesmo). É possível observar também em função da primeira e da segunda derivada.

Vamos calcular a função f(x) em 3 pontos: -1,1; -1 (ponto crítico); -0,9. Teremos então:

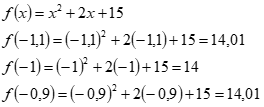
Observe que o ponto crítico possui um valor menor do que em seus arredores. Desta forma no ponto crítico ocorre um valor mínimo, e, logo, esta função neste local, possui concavidade para cima.