Como calcular aproximação e erro por polinomio de Taylor?

1 Fórmula de Taylor A fórmula de Taylor fornece uma aproximação polinomial local cada vez melhor de uma função (muitas vezes) diferenciável à medida que calculamos as suas derivadas. Ela é um pilar fundamental do Cálculo Numérico pois nos ensina como aproximar funções complicadas por funções mais simples. Como uma pequena introdução, vejamos a definição de derivada de uma função real em um ponto x: f ′ (x) = lim h→0 f(x + h) − f(x) h . Uma outra forma de encarar essa definição é observar que ela nos ensina a aproximar a função f perto de x por uma função linear. Isso é facilmente visto manipulando um pouco a expressão acima: f ′ (x) = lim h→0 f(x + h) − f(x) h ⇐⇒ f ′ (x) = lim y→x f(y) − f(x) y − x ⇐⇒ 0 = lim y→x f(y) − f(x) − f ′ (x)(y − x) y − x . Nessa última expressão temos o denominador indo para 0. Normalmente divisões por valores pequenos tendem a gerar valores muito grandes a não ser que o denominador seja menor ainda. Assim a expressão acima nos diz não somente que lim y→x f(y) − f(x) − f ′ (x)(y − x) = 0, Mas que essa expressão vai a zero "mais rapidamente"do que y pode ir para x. Ou seja f(x) − f ′ (x)(y − x) pode ser usada como uma boa aproximação de f(y) e essa aproximação vai se tornando cada vez melhor a medida que y está próximo de x. Tipicamente isso é escrito como f(y) = f(x) + f ′ (x)(y − x) + o(|y − x|). A notação o(|y − x|) representa uma função que vai para zero mais rapidamente que |y − x|, ou seja que lim y→x o(|y − x|) |y − x| = 0, e que representa o erro que é feito a se usar a aproximação linear f(x) + f ′ (x)(y − x) no lugar de f(y). Outro resultado relacionado é o teorema do valor intermediário ∃z ∈ (x, y), f ′ (z) = f(y) − f(x) y − x . 1 Mas uma vez podemos reorganizar as contas de maneira a ver esse resultado como uma fórmula alternativa de calcular o f(y): ∃z ∈ (x, y), , f(y) = f(x) + f ′ (z)(y − x). Ou seja, se soubermos como encontrar o z, podemos calcular f(y) conhecendo apenas f(x) e f ′ (z). Diferente da fórmula anterior, que apenas aproximava f(y), essa fórmula é exata. Mas o preço que se paga por isso é o fato que não conhecemos z, apenas sabemos que ele está no intervalo (x, y). Essas duas fórmulas podem ser generalizadas de maneira a obter mais informação se tivermos as nossa disposição derivadas de ordem mais altas. Essas são as fórmulas de Taylor, que vocês viram nos cursos de cálculo, e que reproduzimos a seguir. Teorema (Fórmula de Taylor). Seja f : R → R uma função e x um número real no qual as derivadas f ′ (x), f ′′(x), . . . , f (n) (x) existem. Então, se definirmos o polinômio (conhecido como polinômio de Taylor) Pn(y) = f(x) + f ′ (x)(y − x) + f ′′(x) 2! (y − x) 2 + . . . + f (n) (x) n! (y − x) n , vale que lim y→x f(y) − Pn(y) (y − x) n = 0. Outra forma de escrever isso é f(y) = Pn(y) + o(|y − x| n ). Já a variação desse resultado associada ao teorema do valor médio é apresentado abaixo. Nela é possível ver de forma mais explícita o erro. Teorema (Fórmula de Taylor com resto de Lagrange). Seja f : R → R uma função e x, y dois números reais. Se as derivadas f ′ , f ′′ , . . . , f (n+1) estão todas definidas no intervalo [x, y], então existe z ∈ (x, y) tal que f(y) = Pn(y) + f (n+1) (z) (n + 1)! (x − y) n+1 . Os dois resultados acima podem ser generalizados para funções de mais de uma variável, em particular se f : Rn → R e J f(x) é a matriz jacobiana de f , ou seja a matriz definida por J f(x)ij = ∂ fi(x) ∂xj , i = 1, . . . , m, j = 1, . . . , n, vale f(y) = f(x) + J f(x)(y − x) + o(||y − x||). Aproximações de ordem mais alta também são possíveis, mas não vamos usá-las em nosso curso.

Olá!

A aproximação pelo polinômio de Taylor do valor de uma função para um determinado ponto x desconhecido, conhecendo o valor da função em um ponto  x0, é dado pela seguinte fórmula:

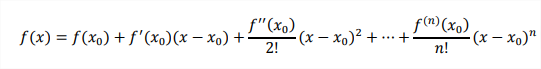
Você pode aproximar este valor para quantos termos n você quiser!

Já a função erro é dada através da seguinte fórmula:

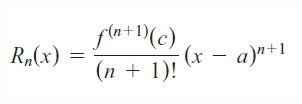
Chamada muitas vezes de "resto".

Bons estudos!