calculo diferencial e integral. preciso de ajuda
Utilizando o conceito de limites para funções de duas ou mais variáveis, encontre o limite da função 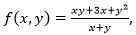 quando x e y tendem respectivamente para 2 e 3.
quando x e y tendem respectivamente para 2 e 3.
💡 5 Respostas
Victoria Alves
Como o ponto (2,3) não causa interminação na função para calcular o limite é só aplicar o valor diretamente.
lim (x,y)→(2,3) (xy+3x+y²)/(x+y)
lim (x,y)→(2,3) (2x3+3x2+3²)/(2+3)
lim (x,y)→(2,3) (6+6+9)/(5) = 21/5
Andre Smaira
---
Vamos calcular o seguinte limite:
\[L=\lim\limits_{(x,y)\to(2,3)}\dfrac{xy+3x+y^2}{x+y}\]
A forma mais simples de se calcular limite de duas variáveis é usando coordenadas polares. Vamos começar por transladar o limite de forma que estudemos a origem:
\[(X,Y)=(x-2,y-3)\]
Assim, temos:
\[L=\lim\limits_{(X,Y)\to(0,0)}\dfrac{(X+2)(Y+3)+3(X+2)+(Y+3)^2}{(X+2)+(Y+3)}\]
\[L=\lim\limits_{(X,Y)\to(0,0)}\dfrac{(XY+2Y+3X+6)+(3X+6)+(Y^2+6Y+9)}{(X+2)+(Y+3)}\]
\[L=\lim\limits_{(X,Y)\to(0,0)}\dfrac{XY+8Y+6X+Y^2+21}{X+Y+5}\]
Vamos agora mudar para coordenadas polares:
\[(X,Y)=(r\cos\phi,r\sin\phi)\]
Então:
\[L=\lim\limits_{r\to }\dfrac{r^2\sin\phi\cos\phi+8r\sin\phi+6r\cos\phi+r^2\sin^2\phi+21}{r\cos\phi+r\sin\phi+5}\]
Substituindo \(r=0\) na expressão, temos:
\[L=\dfrac{21}5\]
---
Como o resultado independe da direção \(\phi\) de aproximação, o limite existe e resulta em:
\[\boxed{\lim\limits_{(x,y)\to(2,3)}\dfrac{xy+3x+y^2}{x+y}=\dfrac{21}5}\]
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Materiais relacionados
 185 pág.
185 pág. 3 pág.
3 pág.





Compartilhar