assinale a alternativa que apresenta o valor correto, respectivamente, de: limx→1−f(x); limx→2−f(x); limx→3f(x)

Atente para a afirmação:

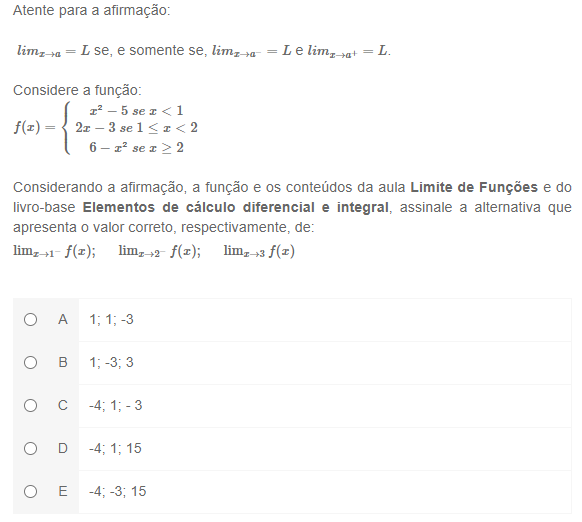
 limx→a=L se, e somente se, limx→a−=L e limx→a+=Ll.

Considere a função:

f(x)=⎧⎪⎨⎪⎩x²−5 se x<12x−3 se 1≤x<26−x² se x≥2f(x)={x²−5 se x<12x−3 se 1≤x<26−x² se x≥2

Considerando a afirmação, a função e os conteúdos da aula Limite de Funções e do livro-base Elementos de cálculo diferencial e integral, assinale a alternativa que apresenta o valor correto, respectivamente, de:

limx→1−f(x);     limx→2−f(x);     limx→3f(x)