Use as coordenadas cilíndricas para determinar o volume do sólido que é limitado pelo cilindro x² + y² = 1 e pela esfera x² + y² + z² = 4?

O exercício pede para calcular o volume de um sólido limitado por: x2+y2> 1 (exterior ao cílindro) e x2+y2+z2<4 (interior a esfera de raio 2).

A imagem abaixo ilustra a situação do enunciado:

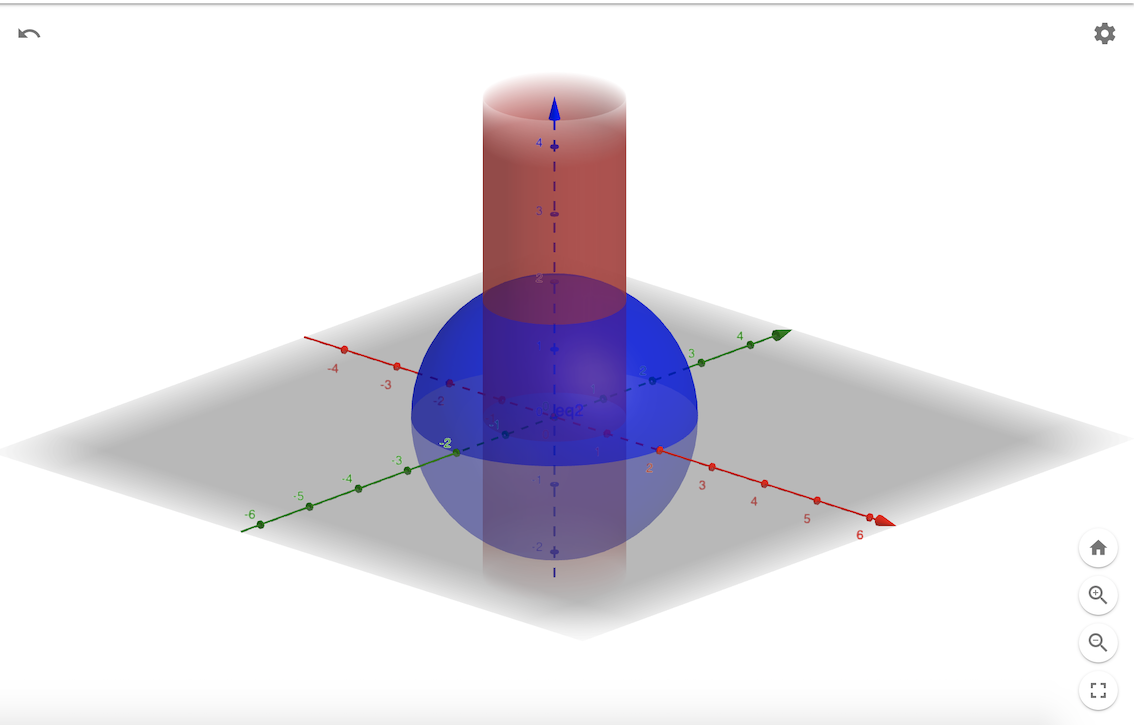
Vamos realizar a mudança de coordenadas cartesianas para coodenadas cilindricas.

x=r*cosθ

y=r*senθ

z=z

Agora é necessário definir os extremos de integração:

1. 0<θ<2π (desejamos pegar a volta inteira)

2. 0<z<√3

Vou integrar somente a parte superior do gráfico, por isso o extremo inferior é 0.

Para achar o extremo superior basta substiuir a equação do cilindro na equação da esfera e ver onde elas se interceptam. Substituindo: 1+z2=4 -> z=√3 (positivo, pois quero a parte de cima)

3. 1<r<√(4-z2)

Conforme explicado, a região de integração é exterior ao cilindro (por isso extremo inferior =1) e interior a esfera. Para achar o extremo superior substituimos x=rcos(θ) e y=rsen(θ) na equação da esfera. Com isso, obtemos uma expressão de r que depende de z.

4. Não podemos nos esquecer do Jacobiano, o qual vale r, para as coodenadas cilindricas.

Finalmente, substituimos na integral e obtemos:

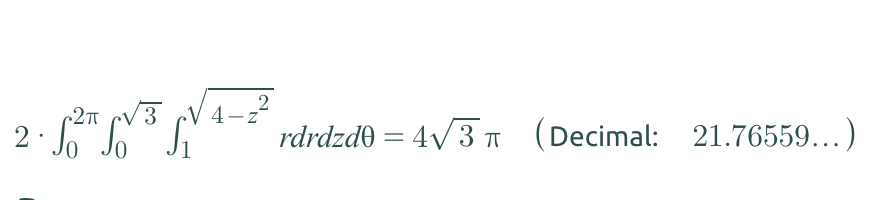
Note que necessariamente, temos que integrar r antes de z, pois r é uma função de z (verifique o Teorema de Fubini)