Resistencia dos Materiais
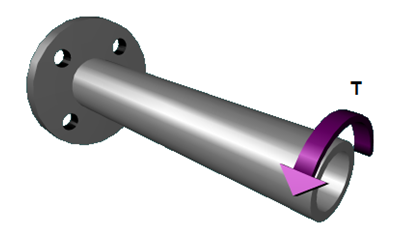
Assinale a alternativa que apresenta o valor do torque T que causa uma tensão cisalhante máxima de 75 MPa em um cilindro de aço de diâmetro externo de 25 mm e espessura da parede 2,5 mm, conforme ilustrado abaixo.
💡 5 Respostas
Claudio Roberto Vieira
135,85 n.m
Adriano Silva
Algum cara dos bons aí pra responder essa do meu amigo?
Luiz -
Olá. Sou o Luiz, estou graduando em eng civil e resolvo questões de diversas matérias da área de exatas. Muitos da Uniube já utilizaram dos meus serviços e continuo procurando por alunos. Se interessar, entre em contato pelo whatsapp: 31 98464-2756. Abç
Faça como milhares de estudantes: teste grátis o Passei Direto
Esse e outros conteúdos desbloqueados
16 milhões de materiais de várias disciplinas
Impressão de materiais
Agora você pode testar o
Passei Direto grátis
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Compartilhar