Respostas
Laís Vargas
Dados os pontos A = (-1, 0, 1) e B = (5, -2, 0), determine as coordenadas de um ponto P, contido no segmento AB, tal que
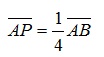
alternativas
| P = (1/2, -1/2, 3/4) | ||
| P = (2, -1, 1/2) | ||
| P = (1, -1/2, 1/4) | ||
| P = (1/2, 3/2, -5/3) | ||
| P = (7/2, -3/2, 1/4) |
Gabriela Teixeira
Como que faz esse calculo ?
RD Resoluções
Assumindo que o exercício pedido é o mesmo contido nesse material, vamos começar com a definição de P:
\(P=(x,y,z),\ \ \bar{AP}={1\over4}\bar{AB}\)
Escrevendo no formato vetorial, temos:
\((x+1,y-0,z-1) = {1\over4}(5+1,-2-0,0-1)\)
O que nos leva às seguintes equações:
\(x+1={6\over4}={3\over2}\\ y=-{2\over4}=-{1\over2}\\ z-1=-{1\over4}\)
Resolvendo-as, temos:
\(x={1\over2}\\ y=-{1\over2}\\ z={3\over4}\)
Logo temos o ponto procurado:
\(\boxed{P=\left({1\over2},-{1\over2},{3\over4}\right)}\)
Responda
Para escrever sua resposta aqui, entre ou crie uma conta







