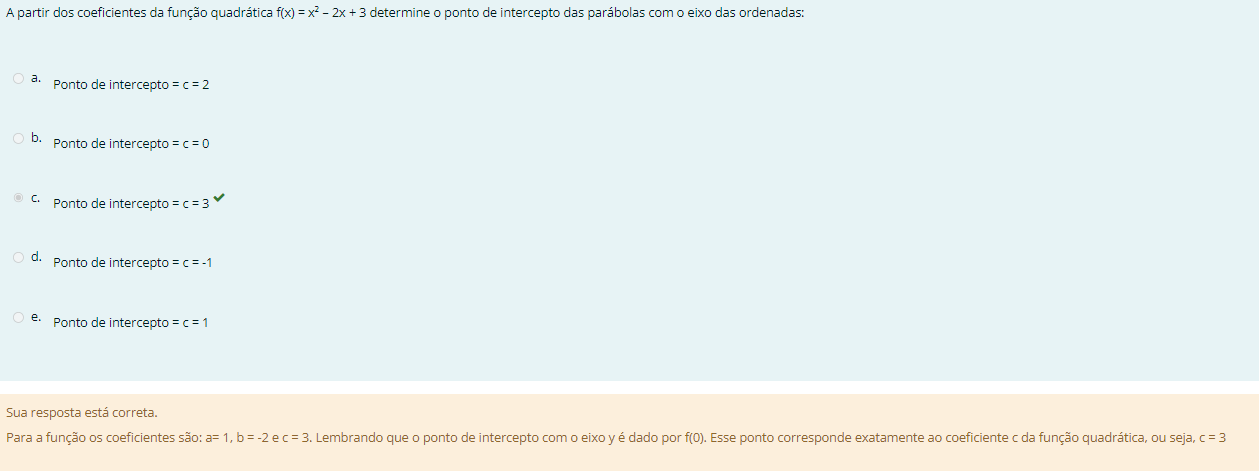
Para encontrar o ponto de intercepto da parábola com o eixo das ordenadas (eixo y), precisamos avaliar a função quadrática \( f(x) = x^2 - 2x + 3 \) quando \( x = 0 \). Substituindo \( x \) por 0 na função: \[ f(0) = (0)^2 - 2(0) + 3 = 3 \] Portanto, o ponto de intercepto com o eixo das ordenadas é \( c = 3 \). Assim, a alternativa correta é: a. Ponto de intercepto = c = 3.