como calcular essa questão?integral passo a passo !! me ajudem
determine a area da regiao limitada pelo grafico de f(x)= 3x+1, pelas retas verticais x=-1 e x=5 e pelo eixo Ox. indique graficamente.
💡 1 Resposta
Maurício Bittencourt Pimenta
Para calcular a área da região, precisamos primeiro calcular em que pontos a função f(x) dada intercepta o eixo Ox. Para isso, igualamos a função a zero:
f(x) = 3x+1 = 0 --> 3x = -1 --> [x = -1/3]
A função f(x) é crescente, pois o coeficiente angular da mesma é positiva. (Em uma função do primeiro grau, na forma f(x) = ax + b, onde a e b são números reais, a é denominado o coeficiente angular da reta e determina se a função é crescente ou decrescente. 'b' é denominado o coeficiente linear e indica o ponto (0,b) do gráfico, onde a reta intercepta o eixo y.)
Podemos, se quisermos, desenhar o gráfico da função f(x) = 3x+1:
http://www.bbc.co.uk/staticarchive/decc09eee0992979cdd751c8563380446a6f8834.gif
Olhando o gráfico, percebemos que a função fica abaixo do eixo Ox quando x < -1/3. Logo, podemos determinar como o ponto mínimo do intervalo que queremos calcular a integral para encontrar a área como [x = -1/3]. O ponto máximo do intervalo, que será o limite superior da integração, será o ponto x = 5, pois queremos a área delimitada pela reta x = 5.
Assim, podemos calcular a área da região como a integral da função f(x) no intervalo [-1/3 , 5].
Teremos:
∫ f(x) = ∫ (3x+1) (Usando a propriedade que: ∫( g(x) + h(x) ) = ∫g(x) + ∫h(x) e
considerando g(x) = 3x e h(x) = 1)
Teremos que:
∫(3x + 1) = ∫3x + ∫1
- A integral de a*(x^b) é igual a: [a/(b+1)]*x^(b+1)
A fórmula escrita assim parece pior do que na prática! hahahaha
Na prática, para integrar, basta somar '1' à potência do x e dividir o número que multiplica o x pela nova potência do x. Exemplo: ∫x² = (x³)/3 e ∫x = (x²)/2
Assim, teremos:
∫3x = (3/2)x² e ∫1 = ∫1*(x^0) = x
Logo:
∫(3x + 1) = ∫3x + ∫1 = (3/2)x² + x
Como temos que calcular a integral definida no intervalo [-1/3 , 5], teremos:
[(3/2)x² + x] (no intervalo [-1/3, 5 ]) = { [ (3/2)(5)² + (5) ] - [ (3/2)(-1/3)² + (1/3) ] }
fazendo o restante dos cálculos, teremos o resultado final:
{ [ (3/2)(5)² + (5) ] - [ (3/2)(-1/3)² + (1/3) ] } = 252/6 = 42
Esse é o resultado final. Espero que tenhas entendido tudo direito. Qualquer dúvida, pode perguntar. :)
E se gostou da resposta, dá um joinha aí e recomenda a resposta! =D
Valeu!
RD Resoluções
Neste exercício, será determinada a área \(A\) limitada por \(y = 3x+1\), \(x=-1\), \(x=5\) e \(y_0=0\) (eixo Ox). Ou seja, será calculada a seguinte integral:
\(\Longrightarrow A= \int \limits_a^b f(x) \space dx \)
Com \(a=-1\), \(b=5\), tem-se que:
\(\Longrightarrow A= \int \limits_{-1}^{5} f(x) \space dx \)
Essa área \(A\) se divide em 2 áreas: uma área \(A_1\) abaixo do eixo Ox e outra \(A_2\) acima do eixo Ox, conforme apresentado na figura a seguir:
Portanto, o valor de \(x_1\) de \(f(x) = 3x+1\) que cruza o eixo Ox é:
\(\Longrightarrow f(x_1) = 3x_1+1\)
\(\Longrightarrow 0=3x_1+1\)
\(\Longrightarrow -3x_1=1\)
\(\Longrightarrow x_1 = -{1 \over 3}\)
Como \(f(x)\) é uma função crescente, o intervalo de \(A_1\) é \(-1 \le x \le x_1\) e o intervalo de \(A_2\) é \(x_1 \le x \le 5\). Portanto, a expressão de \(A\) fica da seguinte forma:
\(\Longrightarrow A= \int \limits_{-1}^{5} f(x) \space dx \)
\(\Longrightarrow A= A_1 + A_2\)
\(\Longrightarrow A= \int \limits_{-1}^{x_1} \Big [y_0 - y \Big ] \space dx + \int \limits_{x_1}^{5} \Big [y - y_0 \Big ] \space dx \)
Com \(x_1 = -{1 \over 3}\), \(y = 3x+1\) e \(y_0=0\), o valor de \(A_1\) é:
\(\Longrightarrow A_1= \int \limits_{-1}^{x_1} \Big [y_0 - y \Big ] \space dx \)
\(\Longrightarrow A_1= \int \limits_{-1}^{-{1 \over 3}} \Big [0 - (3x+1) \Big ] \space dx \)
\(\Longrightarrow A_1= -\int \limits_{-1}^{-{1 \over 3}} (3x+1) \space dx \)
\(\Longrightarrow A_1= \int \limits_{-{1 \over 3}}^{-1} (3x+1) \space dx\)
\(\Longrightarrow A_1= \Big [ 3{x^2 \over 2}+x \Big ]\bigg |_{-{1 \over 3}}^{-1} \)
\(\Longrightarrow A_1= \Big [ 3{(-1)^2 \over 2}+(-1) \Big ] - \Big [ 3{(-{1 \over 3})^2 \over 2}+(-{1 \over 3}) \Big ]\)
\(\Longrightarrow A_1= \Big [ {1 \over 2} \Big ] - \Big [-{1 \over 6} \Big ]\)
\(\Longrightarrow A_1= {2 \over 3}\)
Com \(x_1 = -{1 \over 3}\), \(y = 3x+1\) e \(y_0=0\), o valor de \(A_2\) é:
\(\Longrightarrow A_2= \int \limits_{x_1}^{5} \Big [y - y_0 \Big ] \space dx \)
\(\Longrightarrow A_2= \int \limits_{-{1 \over 3}}^{5} \Big [(3x+1) - 0 \Big ] \space dx \)
\(\Longrightarrow A_2= \int \limits_{-{1 \over 3}}^{5} (3x+1) \space dx \)
\(\Longrightarrow A_2=\Big [ 3{x^2 \over 2}+x \Big ]\bigg |_{-{1 \over 3}}^{5}\)
\(\Longrightarrow A_2= \Big [ 3{(5)^2 \over 2}+(5) \Big ] - \Big [ 3{(-{1 \over 3})^2 \over 2}+(-{1 \over 3}) \Big ]\)
\(\Longrightarrow A_2= \Big [ 42,5 \Big ] - \Big [ -{1 \over 6} \Big ]\)
\(\Longrightarrow A_2= {128 \over 3}\)
Finalmente, o resultado final do exercício é:
\(\Longrightarrow A= A_1 + A_2\)
\(\Longrightarrow A= {2 \over 3} + {128 \over 3}\)
\(\Longrightarrow \fbox {$ A= {130 \over 3} $}\)
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Materiais relacionados
 4 pág.
4 pág.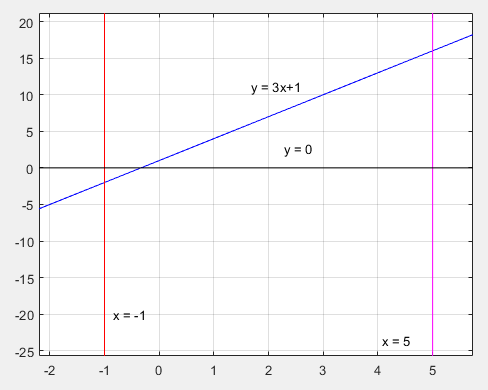




Compartilhar