Metodos Numéricos aplicados Determine o erro absoluto da solução
Sabendo que a solução real da integra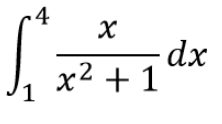
e 1,070033. Determine o erro absoluto da solução
encontrada para essa integral pelo Método dos Retangulos com a altura tomada pela direita, utilizando 3 subintervalos.
A = 0
B = 0,134639
C=14,4%
D= 0,143938
💡 8 Respostas
Andre Smaira
Temos que
\(f(x)=\dfrac{x}{x^2+1}\)
, com limites de integração
\((a,b)=(1,4)\)
. Desejamos repartir o domínio em
\(n=3\)
subintervalos, cada um com comprimento
\(h=\dfrac{b-a}{n}=1\)
.
A área dos retângulos será então
\(A_i=h\cdot f(x_i)\)
. Como tomamos a altura pela direita, temos que
\(x=\{2,3,4\}\)
.
Fazemos então
\(I=\int _1^4 \dfrac{x}{x^2+1}=h\cdot\sum_{i=1}^n f(x_i)\)
.
Assim,
\(I=1\cdot\left( 0,4+0,3+0,23529\right)=0,93529\)
.
O erro será
\(e=1,07003-0,93529=0,13474\)
Assim, a alternativa correta é a letra (b).
Edgar pedro
A resposta corretá é a letra B,tenho certeza!
Hernando Ibarros
Boa Noite.
Alguém pode me ajudar com esta questão?
att
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta
Perguntas relacionadas
Materiais relacionados
 9 pág.
9 pág.






Compartilhar