Como derivar raiz
💡 5 Respostas
Gabriele Mota
Coloque a raiz em forma de fração.
Ex: "Raiz quadrada de 2x" = (2x)^1/2 , logo a derivada fica: 1/2*(2x)^-1/2*2.
Andre Smaira
Contextualização:
Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.
Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação).
Classificação
Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.
Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.
Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.
Exemplos:

, tem ordem 1 e grau 1
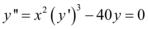
, tem ordem 2 e grau 3
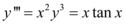
, tem ordem 3 e grau 3
Referência: https://www.somatematica.com.br/superior/equacoesdif/eq.php - Acessado em 12/10/2018
Resolução:
Sabendo que toda raiz, seja ela quadrada ou não é uma função exponencial, exemplo:
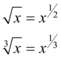
Basta transformar em uma função exponencial, sendo assim podemos considerar a raiz quadrada de x como 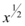 , logo sua derivada será:
, logo sua derivada será:
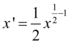
E então:
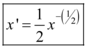
Conclusão:
Portanto, para derivar uma raiz, devemos transformá-la em uma função exponencial. No caso da derivada de 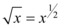 , temos:
, temos:
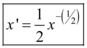
Andre Smaira
Contextualização:
Se y é uma função de x, e n é um inteiro positivo, então uma relação de igualdade (que não se reduz a uma identidade) que envolva x, y, y', y'', ...,y(n) é chamada uma equação diferencial de ordem n.
Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida (a incógnita da equação).
Classificação
Equação Diferencial Ordinária (EDO): Envolve derivadas de uma função de uma só variável independente.
Equação Diferencial Parcial (EDP): Envolve derivadas parciais de uma função de mais de uma variável independente.
Ordem: é a ordem da derivada de mais alta ordem da função incógnita que figura na equação.
Exemplos:
, tem ordem 1 e grau 1
, tem ordem 2 e grau 3
, tem ordem 3 e grau 3
Referência: https://www.somatematica.com.br/superior/equacoesdif/eq.php - Acessado em 12/10/2018
Resolução:
Sabendo que toda raiz, seja ela quadrada ou não é uma função exponencial, exemplo:
Basta transformar em uma função exponencial, sendo assim podemos considerar a raiz quadrada de x como , logo sua derivada será:
E então:
Conclusão:
Portanto, para derivar uma raiz, devemos transformá-la em uma função exponencial. No caso da derivada de , temos:
✏️ Responder
Para escrever sua resposta aqui, entre ou crie uma conta




Compartilhar